国立高専の数学の入試問題は、特殊で難しいイメージを持っている中学生が多いですが、全ての問題が特殊で難しいわけではありません。数学の入試問題の傾向を把握し、適切な対策を行なった上で立ち向かえば、十分に高得点を狙うことができます。
また、国立高専の入試は、令和4年度（2022年度）入試から思考力・判断力・表現力をより重視した作成方針へ移行されましたが、数学の入試問題には以前から思考力等を測れるよう工夫した問題が出されており、入試傾向に大きな変化はありませんでした。そのため、過去問を使った対策は、これまで同様、非常に効果的です。とはいえ、思考力等を測る新傾向問題への対応はしっかりと行う必要があります。
ここでは、高専の数学の入試問題を攻略するために必要な、把握すべき出題傾向や対策方法について紹介していきます。
目次
高専入試数学の出題傾向
高専入試数学の問題構成
国立高専の数学の入試問題は、ここ数年、大問4題で構成されています。
大問1が8問の小問集合、大問2〜4は方程式・関数、図形、規則性の問題などが出題されています。また、大問2〜4の中の設問は、後ろの設問ほど難しい構成になっています。
高専入試数学の頻出分野・問題
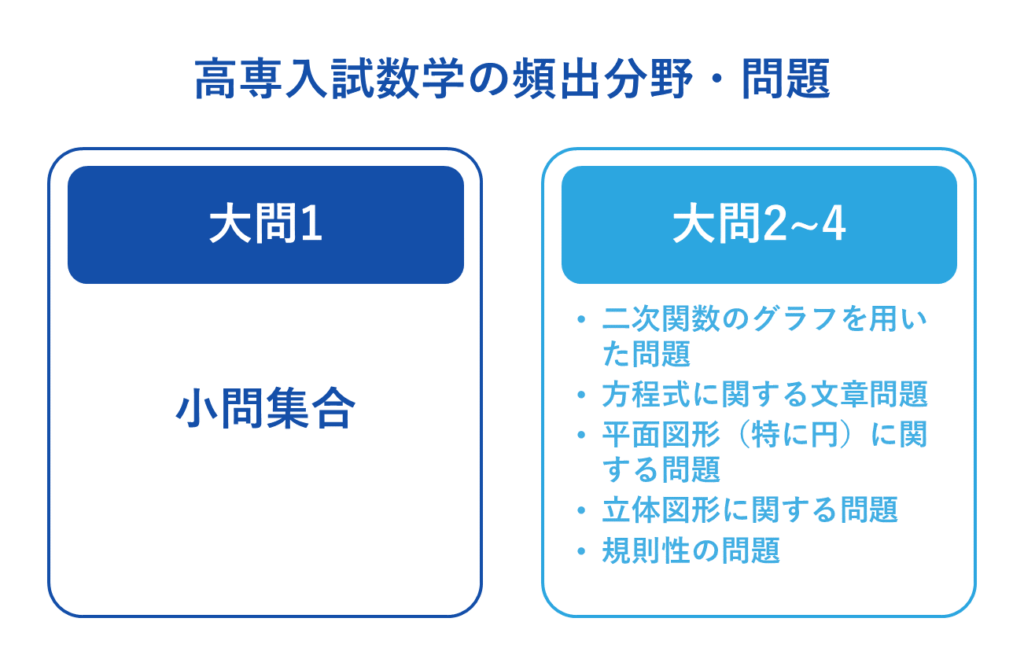
高専入試の数学は、大問1の小問集合では各単元が満遍なく出題され、大問2〜4では、以下の分野の問題が頻出です。
- 二次関数のグラフを用いた問題
- 方程式に関する文章問題
- 平面図形（特に円）に関する問題
- 立体図形に関する問題
- 規則性の問題
近年では、特に規則性の問題で、プログラムを題材にしたり、会話文を用いた問題など、図表や文章といった様々な情報から問題を解くために必要な内容を読み取らせる問題が頻出になってきています。
高専入試数学の配点
高専入試における数学の傾斜配点
高専では、教科ごとの配点が異なる傾斜配点を採用している学校がありますが、特に数学は他の教科に対して配点を高くしている高専が多いです。
数学の配点が2倍の高専
- 苫小牧工業高等専門学校（北海道）
- 函館工業高等専門学校（北海道）
- 旭川工業高等専門学校（北海道）
- 釧路工業高等専門学校（北海道）
- 仙台工業高等専門学校（宮城県）
- 東京工業高等専門学校（東京都）
- 長岡工業高等専門学校（新潟県）
- 長野工業高等専門学校（長野県）
- 津山工業高等専門学校（岡山県）
- 徳山工業高等専門学校（山口県）
- 阿南工業高等専門学校（徳島県）
- 新居浜工業高等専門学校（愛媛県）
- 鹿児島工業高等専門学校（鹿児島県）
- 沖縄工業高等専門学校（沖縄県）
数学の配点が1.5倍の高専
- 茨城工業高等専門学校（茨城県）
- 群馬工業高等専門学校（群馬県）
- 沼津工業高等専門学校（静岡県）
- 鈴鹿工業高等専門学校（三重県）
- 舞鶴工業高等専門学校（京都府）
- 大阪公立大学工業高等専門学校（大阪府）
- 明石工業高等専門学校（兵庫県）
- 神戸工業高等専門学校（兵庫県）
- 久留米工業高等専門学校（福岡県）
- 熊本高等専門学校（熊本県）
高専入試の数学の問題配点
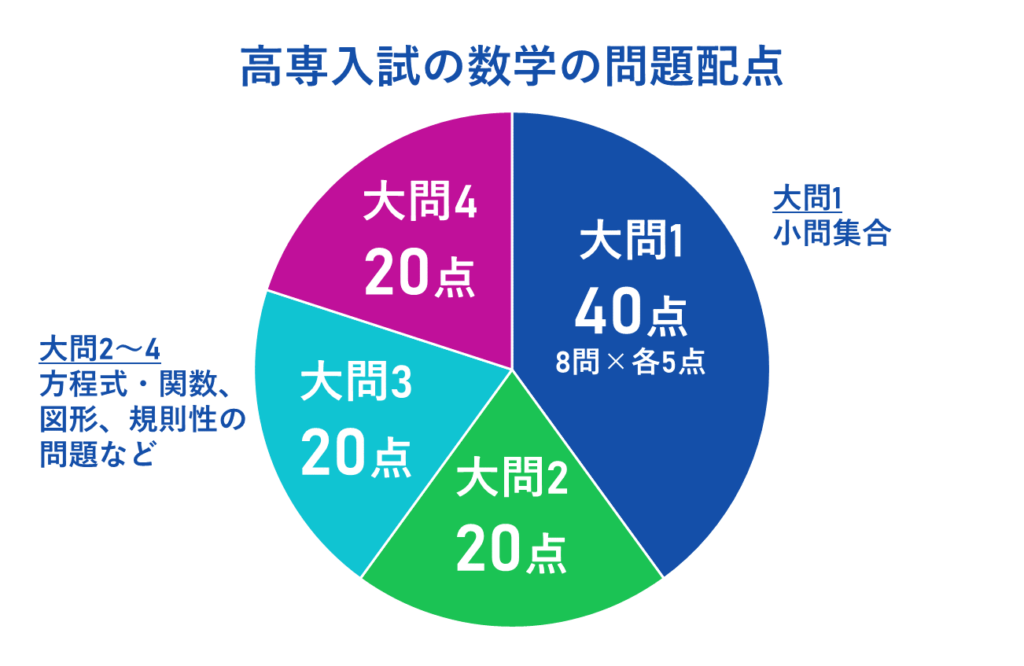
配点は、大問1が設問各5点の計40点、大問2〜4はそれぞれ20点です。
基本問題が多い小問集合に全体の40％の配点があるため、大問1は必ず全問正解しておきたいところです。
高専入試数学の実際の問題例
高専入試の数学で実際に出題された問題を紹介します。
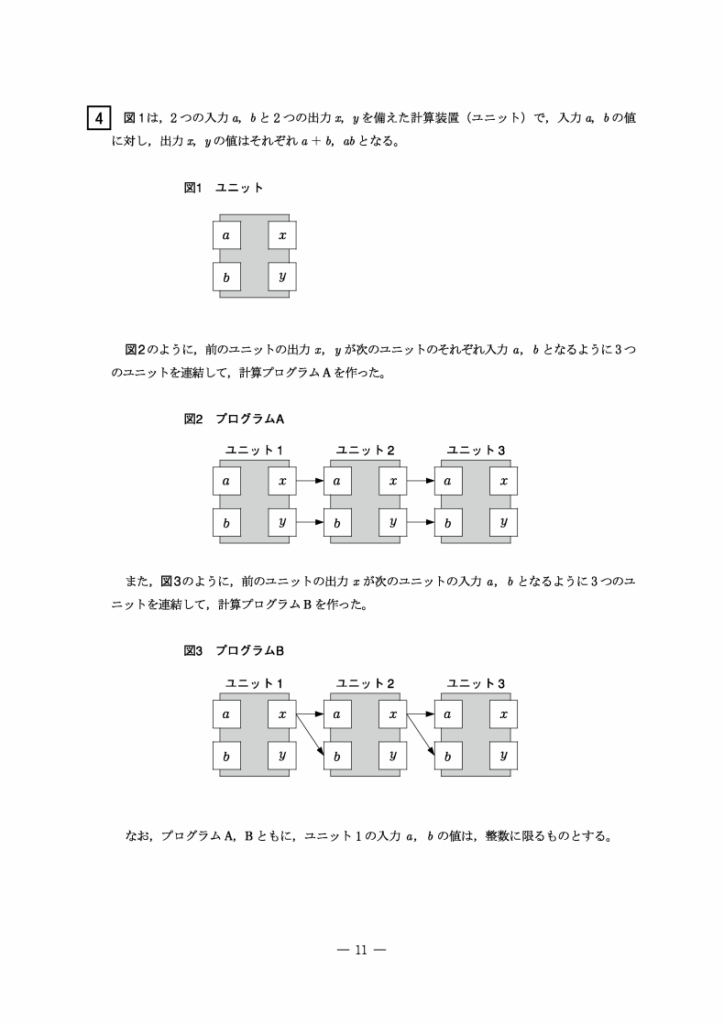
以下の問題は、令和4年度入試の数学（本試験）の大問4です。
入力と出力を2つずつ持つ計算装置（ユニット）を使ったプログラムに関する問題です。
いきなり「計算装置」や「プログラム」といった語句が出てくると慌ててしまう受験生もいますが、問題文と図を読み解いて丁寧に整理すれば、関数と代入の関係として把握することができます。
文章や図といった与えられた情報を数学的に捉えられるかどうかが鍵となりますが、個々の計算難易度はそれほど高くありません。
もう1題紹介しましょう。
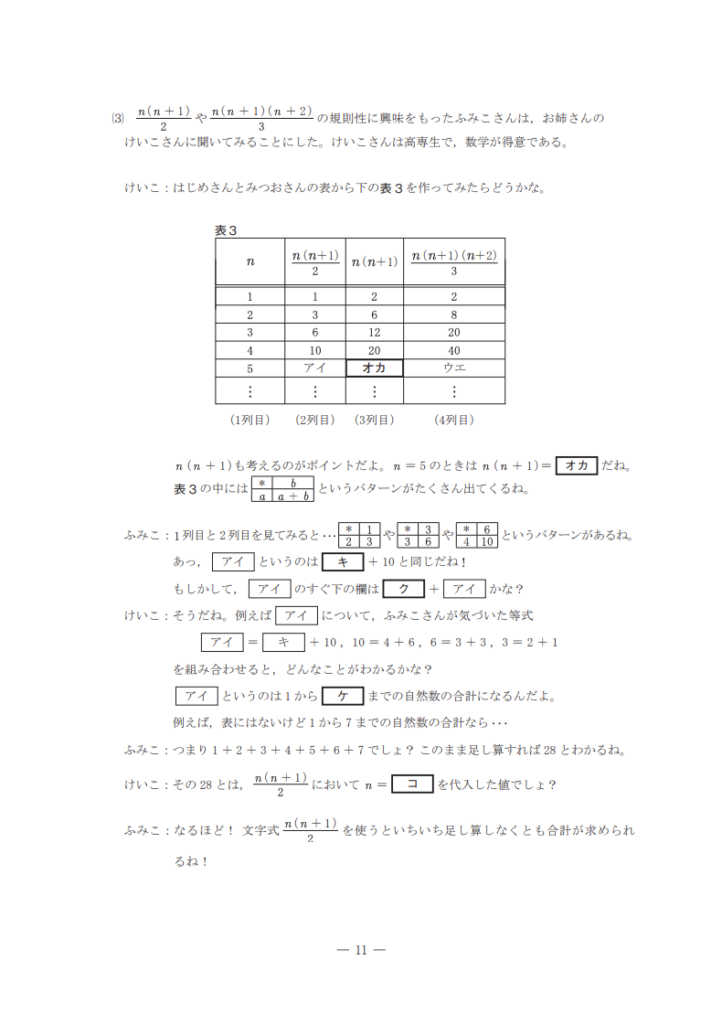
以下の問題は、令和6年度入試の数学（本試験）の大問4です。
こちらは高専数学の頻出分野である規則性の問題です。
この問題で特徴的なのは、はじめさんとふみこさんの会話形式で進む点です。設問は3つのみですが、会話文と表で4ページにも渡るため、初見で敬遠してしまう受験生も多いかと思います。
ただ、特別なひらめきや発想が必要なわけではなく、会話と表を丁寧に読み取って整理することができれば、規則性の把握自体は難解なものではありません。
確かに後半部分の難易度は高めですが、捨て問になるようなレベルではありません。
小問集合や大問2〜4の前半の設問をスピーディに解いて、後半の設問を腰を据えてじっくり解くことができれば、十分に対応可能です。
高専入試数学の公立高校との出題傾向の違い
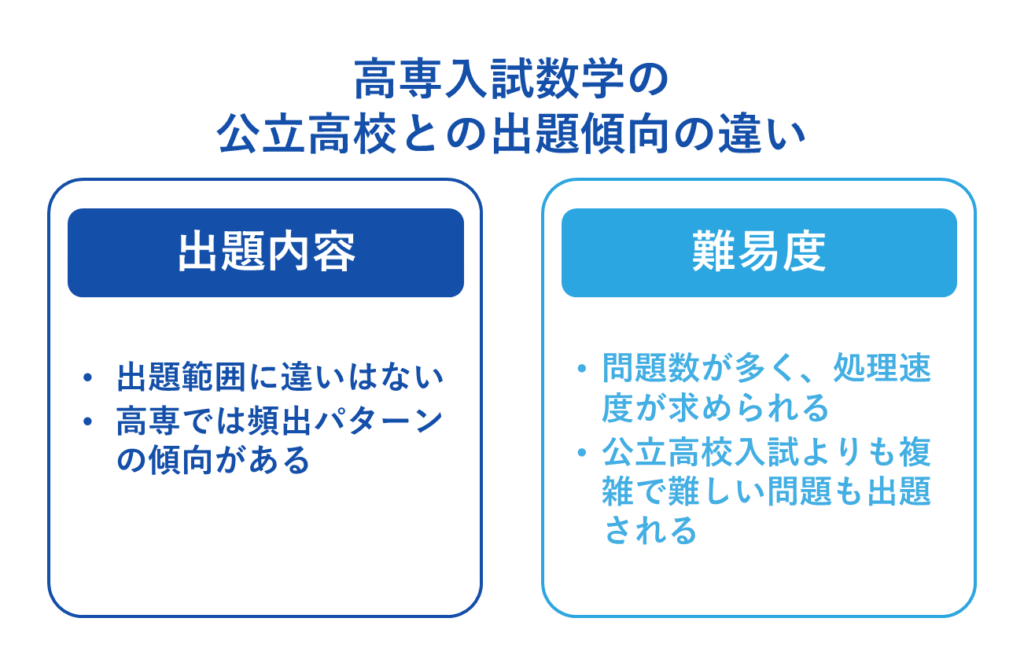
高専と公立高校数学の出題内容の違い
高専入試と公立高校入試の数学で出題範囲に違いはありません。
一方で、上述したように大問2〜4については、高専では頻出パターンの傾向がありますので、都道府県にもよりますが、高専入試と公立高校入試の数学の出題内容が異なります。
高専と公立高校数学の難易度の違い
高専の数学について、難問ばかりが出題されるようなイメージを持たれている生徒さんや保護者の方もいらっしゃいますが、実は一部複雑であったり高専特有の問題が出題されるものの、小問集合を含め学校の教科書レベルの出題が多くを占めています。ただし、問題数が多く、処理速度が求められる点や、大問2〜4の後半の設問では、公立高校入試で出題される問題よりも複雑で難しい問題も出題されています。
とはいえ、特別なひらめきや発想が必要な問題ではなく、問題文や与えられた資料を正確に読み取り、数学的（論理的）に把握し、処理することができれば十分対応可能です。
高専入試数学の対策方法
高専入試数学の対策スケジュール
1年開始
中学1年生から高専入試数学の対策を行う場合は、まず学校授業で進めている内容について抜け漏れが出ないように仕上げていきましょう。
授業毎に復習し、テスト勉強でも教科書やワークレベルの問題はすらすら解ける状態にすることに取り組んでいってください。
その上で説明や解説が充実した教材や動画付き教材で中学3年間の範囲について基本内容の予習を行うことをお勧めします。つまり高専入試数学の出題範囲の全体学習を行います。完璧に理解し、解けるようにするのが理想的ですが、まずは内容の理解をすることから始めていきましょう。
2年開始
中学2年生から対策を行う場合は、まず中1の学習内容の復習から始めていきましょう。教科書やワークの基本問題を解き進めていって、解き方を忘れている箇所を見つけたら、教科書で思い出し→演習で解けるようにする、の繰り返しで進めていきましょう。
ここまでできたら、次は中学3年間の範囲について、基本内容の予習を進めていきましょう。
3年開始
中学3年生から行う場合は、中学3年間の範囲について、受験用の総復習教材を進めてみましょう。いきなり受験レベルの問題集に入る必要はありません。既習範囲については問題をすらすら解けるレベル、未習範囲については内容の理解、問題の解き方の理解をすることを重視して進めてください。
学校で習ってからでないと進めにくいという意見もありますが、高専の入試数学は問題数が多く難易度が高い問題もあり、傾斜配点で1.5倍から2倍換算されるところもありますので、早い段階で出題範囲全体の予習も含めて、受験対策を進めていきましょう。
高専ならではの数学対策
国立高専の入試問題は全てマーク式ですが、導出過程の計算式や数値を答えさせる問題が多いため、実は導出過程を記述する対策も効果的です。
また、導出過程の計算式や数値を答えるような問題の対策としては、解説が詳しい教材で解説をしっかりと読み込むこともおすすめです。
問題集の解説は、解答に至るまでの流れを文章や計算過程で説明しており、高専のマーク式問題の空欄の前後に当たる部分が多いです。そのため、空欄を埋める形式の問題で、解答に至るまでの流れを把握するのに適しています。
答え合わせや解法の理解だけでなく、高専のマーク式問題対策のためにも、ぜひ利用してみて下さい。
導出過程の見直し対策も必須です。
マーク式なので、部分点はありません。途中の計算式や数値が１つでも間違っていると失点、さらに以降の問題まで全て間違えてしまう可能性があります。計算式中の数値や途中で利用するために導出した数値のミスにも気をつけながら取り組みましょう。
また、以下の頻出問題の対策は重点的に行うことが必須です。
- 二次関数のグラフを用いた問題
- 方程式に関する文章問題
- 平面図形（特に円）に関する問題
- 立体図形に関する問題
- 規則性の問題
高専の数学では、文章量が多い問題も出題されています。
高専の入試対策で、国語に力を入れる受験生はあまり多くありませんが、高専の入試数学では読解力を要する問題も多く出題されており、国語の読解対策もしっかり行っていきましょう。
過去問を使った高専数学対策
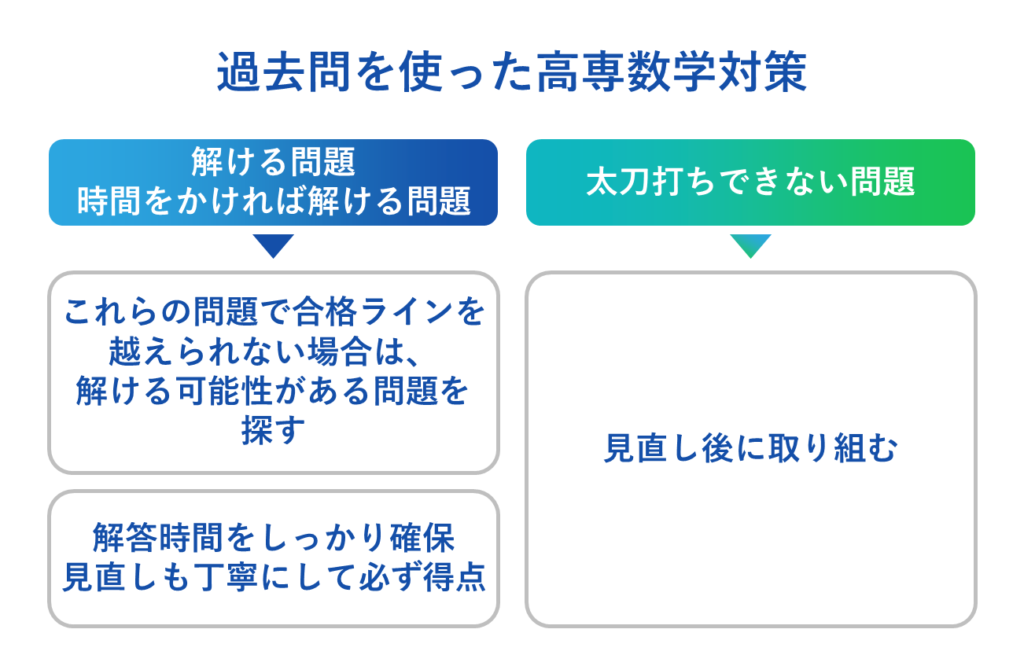
過去問を使った数学対策の方法は以下の通りです。
過去問は「傾向の把握と分析」「演習」「復習」の段階に分けて取り組んでいきましょう。
高専の入試、数学では、上述した通り問題番号ごとに難易度の規則性があります。現在の自分の力で解ける問題、解ける可能性がある問題はどの大問のどの設問なのか、逆に太刀打ちできない問題はどの大問のどの設問なのか、問題や構成の傾向把握、分析を行いましょう。
その上で、自分が得点しないといけない問題、時間をかけて良い問題、見直しをしてから取り組む問題に分けて、どの問題を優先して解答するのか、どの問題まで解答できる様に時間を使うのか、といった試験戦略を立てておくことが大切です。高専によって必要な得点は異なります。自分が数学でどのくらいの得点を取らないといけないのかを明確にして、合格するために、どのレベルの問題まで解かないといけないのか、解ける問題をどのくらいの時間で解き切らないといけないのか、しっかりと整理しておきましょう。
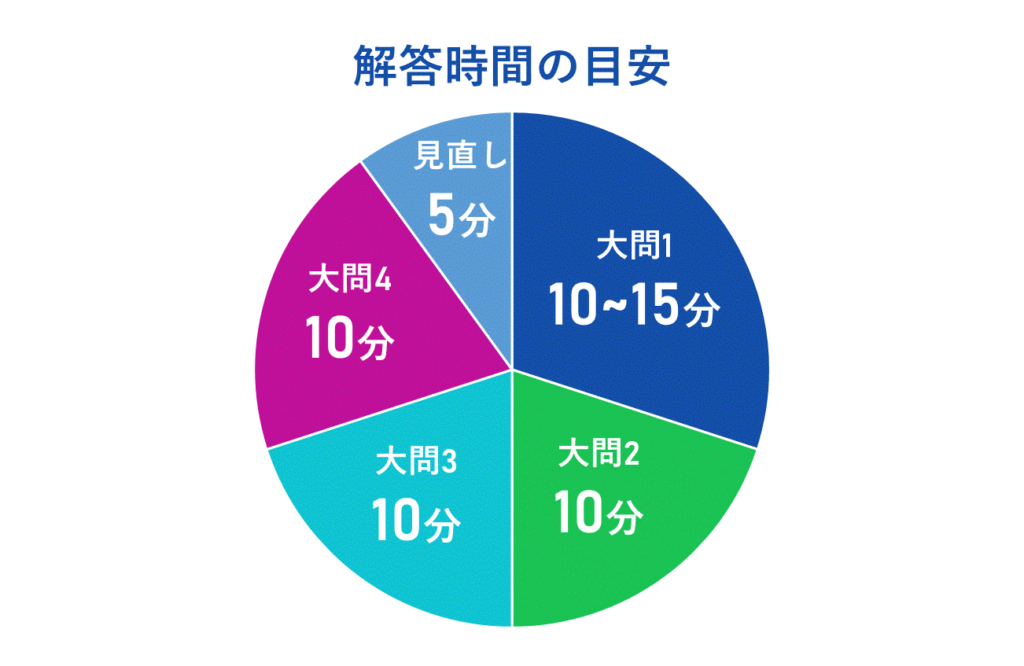
試験時間は50分ですので、全問解くことを目指す場合、解答時間の目安は、大問1：10〜15分、大問2〜4：各10分、見直し時間5〜10分を目安として微調整すると良いでしょう。
演習では、立てた試験戦略に沿って時間を測って過去問を解いていきましょう。解いた後は、必ず解答の答え合わせ、見直しを行うとともに、試験戦略の微調整が必要かどうか検討しましょう。どの様に時間配分をしていたらよかったか、見直し時間の取り方や見直す問題が適切だったかなど、振り返りを行うことで試験戦略をブラッシュアップして、今の実力で取れる点数を最大化させましょう。
復習では、基本的に演習と同様ですが、ある程度問題内容を把握できている状態でしたら、解答時間を30〜40分程度に設定して練習してみても良いでしょう。
高専入試対策をご希望の方へ
公立高校に合格できる学力に加えて、高専受験に特化した専門的な学習にも取り組みたい方にはじゅけラボ予備校の高専受験対策講座がおすすめです。今から高専合格に向けて勉強したい方を、志望高専合格まで最短ルートで導きます。中３だけでなく中１・中２から高専対策に取り組む事で高専の推薦入試での合格率が大きく高まります。
