2025年共通テスト数学対策
2024年度大学入学共通テスト
数学の傾向から考察

ここでは大学入学共通テスト・数学の出題傾向・対策などを解説していきます。共通テストの傾向をしっかりと把握して正しい共通テスト対策を行っていきましょう。
ここでは大学入学共通テスト・数学の出題傾向・対策などを解説していきます。共通テストの傾向をしっかりと把握して正しい共通テスト対策を行っていきましょう。
2024年度共通テスト数学の解説
2024年度共通テストの数学はどのような傾向になっていたのか。項目ごとに解説します。
2024年度共通テスト数学の平均点(ⅠA・ⅡB)と2023年からの推移
2024年度大学入学共通テストの数学は、前年度の易化に対し、平均点は数学1A、数学2Bともに下がっていますが、難易度としてはおおよそ同じだったと言えるでしょう。
2024度共通テスト数学の難易度は?
| 科目 | 満点 | 2024年度 平均点 |
2023年度 平均点 |
前年度との差 |
|---|---|---|---|---|
| 数学ⅠA | 100 | 51.38 | 55.65 | ▲4.27 |
| 数学ⅡB | 100 | 57.74 | 61.48 | ▲3.74 |
共通テスト数学の問題傾向と2025年度の予想
2022年度の共通テスト数学は前年の2021年度と比較して大幅に難化し、それに対して2023年度は易化しました。2024年度は平均点が少し下がったものの、難化、易化の流れから調整がうまく行われ、2025年度はこの難易度に落ち着くと予想されます。
文章量が減り、公式や定義を理解していれば解答できる問題が増えました。また、簡単な問題から難しいものに順に出題されたような大問もあり、得点しやすかったと考えられます。
2024年度共通テスト数学 配点
2024年度共通テスト数学の大問ごとの配点は下記のとおりです。
数学Ⅰ・A
昨年の共通テスト同様に、必答問題が2題・選択問題3題から2題の選択の合計4題を解答する形での出題でした。
2023年度共通テスト数学Ⅰ・A 大問ごとの配点
| 大問 | 内容 | 配点 |
|---|---|---|
| 1 | (1)数と式 | 30 |
| (2)図形と計量 | ||
| 2 | (1)データの分析 | 30 |
| (2)二次関数 | ||
| 3 | 場合の数と確率 | 20 |
| 4 | 整数の性質 | 20 |
| 5 | 図形の性質 | 20 |
※大問3〜5から2題選択
数学Ⅱ・B
大問構成は昨年と同様。選択問題も確率分布、数列、ベクトルとこれも前年同様でした。
2023年度共通テスト数学Ⅱ・B 大問ごとの配点
| 大問 | 内容 | 配点 |
|---|---|---|
| 1 | (1)三角関数 | 30 |
| (2)指数・対数関数 | ||
| 2 | (1)微分・積分法 | 30 |
| (2)微分・積分法 | ||
| 3 | 確率分布・統計 | 20 |
| 4 | 数列 | 20 |
| 5 | ベクトル | 20 |
※大問3〜5から2題選択
2025年度共通テスト数学の対策
共通テスト 数学の問題傾向や時間配分などをお伝えしてきました。
それではどのように準備をしていけばよいのでしょうか。
共通テスト数学で高得点を取るためのおすすめの勉強法

ここでは、共通テスト 数学で高得点をとるためのおすすめの勉強法を紹介します。
まずは基礎基本の徹底
共通テストの内容を見てみると、基礎的な内容から発展させた構成の出題が多くみられます。普段の学習で基礎的な内容を身につけていることはもちろん、発展的な内容を類推することが大切である。幅広いレベル・ジャンルの問題演習に繰り返し取り組みましょう。
できない分野をつぶす
幅広い分野から偏りなく出題されるため、苦手分野を残すと得点に響きます。基礎的な事項から丁寧に理解し、演習を繰り返し、苦手分野をなくしましょう。
難しい問題集より、簡単な参考書を徹底する
共通テストに限らず、入試は教科書の範囲からの出題が基本です。難解な問題集にチャレンジするよりも、基本的な問題集・参考書を徹底的に理解するほうが、結局高得点に繋がります。
個別試験を見通した対策が重要
個別試験に数学がある受験生の場合、共通テストから個別試験を通して対策計画を立てることが重要です。共通テスト対策は個別試験対策につながる部分が多いため、共通テスト対策を土台として、個別試験の傾向に合わせた対策へ移行していくのが良いでしょう。共通テストの直前期になったら共通テストの過去問に取り組みましょう。
共通テスト模試、予想問題集、過去問を利用
基礎を抑えたら、次に演習です。その際には共通テスト模試や予想問題集、共通テストの過去問にも積極的に取り組みましょう。共通テストとセンター試験は傾向が異なる部分もありますが、センター試験で出題されていた問題自体は良問が多く、十分参考になります。
時間内に問題解決に導けるスピードを身につけるため、時間を測りながらの演習も必須です。
文系の受験生はいつから共通テスト対策に取り組むべきか
文系の生徒の場合、基礎基本ができているという前提ですが、個別試験で数学があれば春から、ない場合でも夏ぐらいから取り組みましょう。多様な題材(予想問題集や過去問など)を活用して演習に取り組みましょう。直前期でいいというアドバイスがされることもありますが、早めに取り組み問題のパターンやスピードに慣れておくことをおすすめします。
共通テスト数学 直前対策
共通テスト直前になったら、できなかった問題を繰り返しやり、確実に解けるようにしておきましょう。何度も間違ってしまう問題は、基本的なことが理解できていない可能性があります。放置すると他にも解けない問題が出てくる可能性があるため、さかのぼって復習することも忘れずに。
また、過去問や模試を使っての時間配分の確認も重要です。数学IIBは問題ページが大幅に増え、解くスピードが求められるようになりました。今年も同じ傾向が続くとするなら、スピードアップは大事なポイントになります。
せっかく解ける問題を時間切れで解けないのはもったいないので、時間内に解ききることができるようにトレーニングをしておきましょう。
共通テスト数学 対策問題集・参考書(文系・理系共通)
基礎基本を固めた上で読解力・理解力が求められていることを踏まえて、共通テストの傾向に沿った解説・アドバイスをしてくれる教材を吟味して、徹底的に使い倒しましょう。
人気の参考書やオリジナルで制作されたものなどが悪いわけではありませんが、自分の実力にあったものを徹底するほうが地力はつきます。
2025年度共通テスト数学 時間配分
共通テストは読解量が多くなり、時間がタイトになっている傾向にあります。ここでは時間配分の例を紹介します。
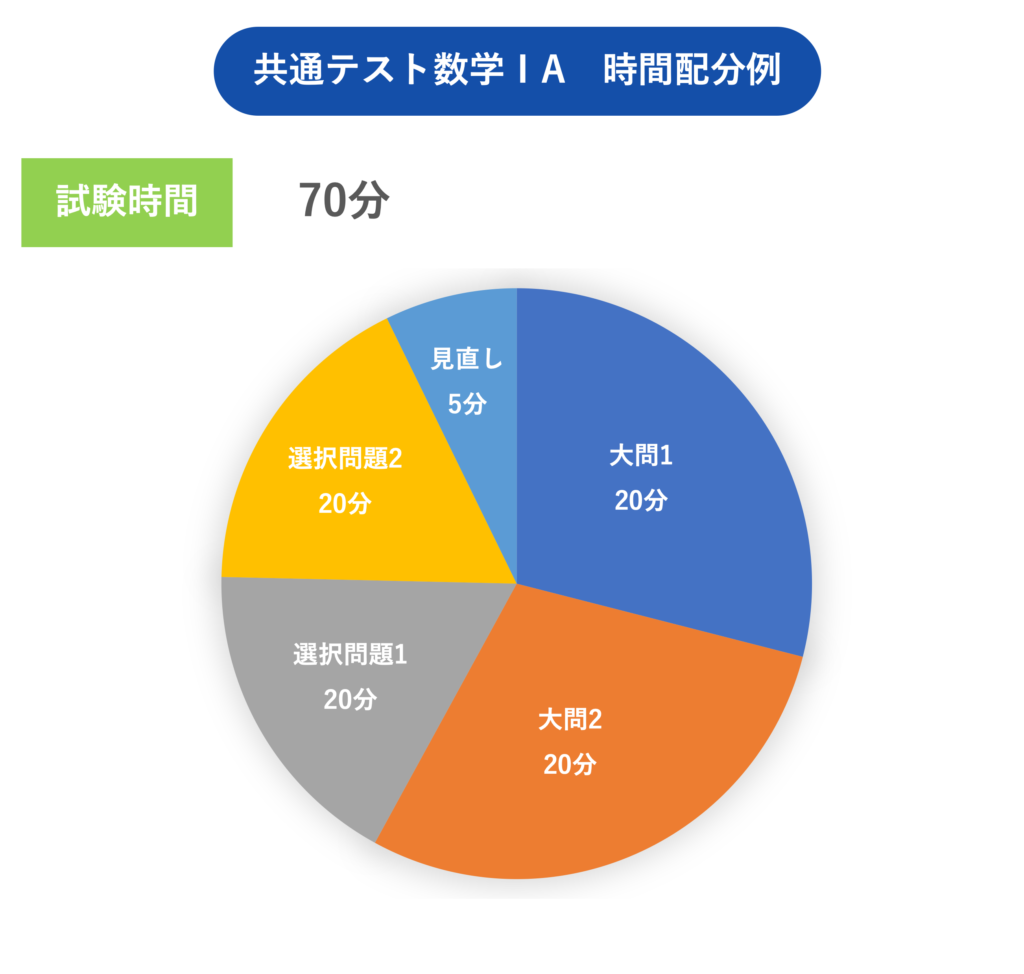
共通テスト数学ⅠA 時間配分例
数学IA時間配分例は、下記のとおりです。
試験時間は70分です。
見直し・チェックすることを考えると、それぞれであと1〜2分は縮めたいところです。
数学ⅠA 時間配分例
| 大問1 | 20分 |
|---|---|
| 大問2 | 20分 |
| 選択問題1 | 12分前後 |
| 選択問題2 | 12分前後 |
| 見直し | 5分 |
| 計 | 70分 |
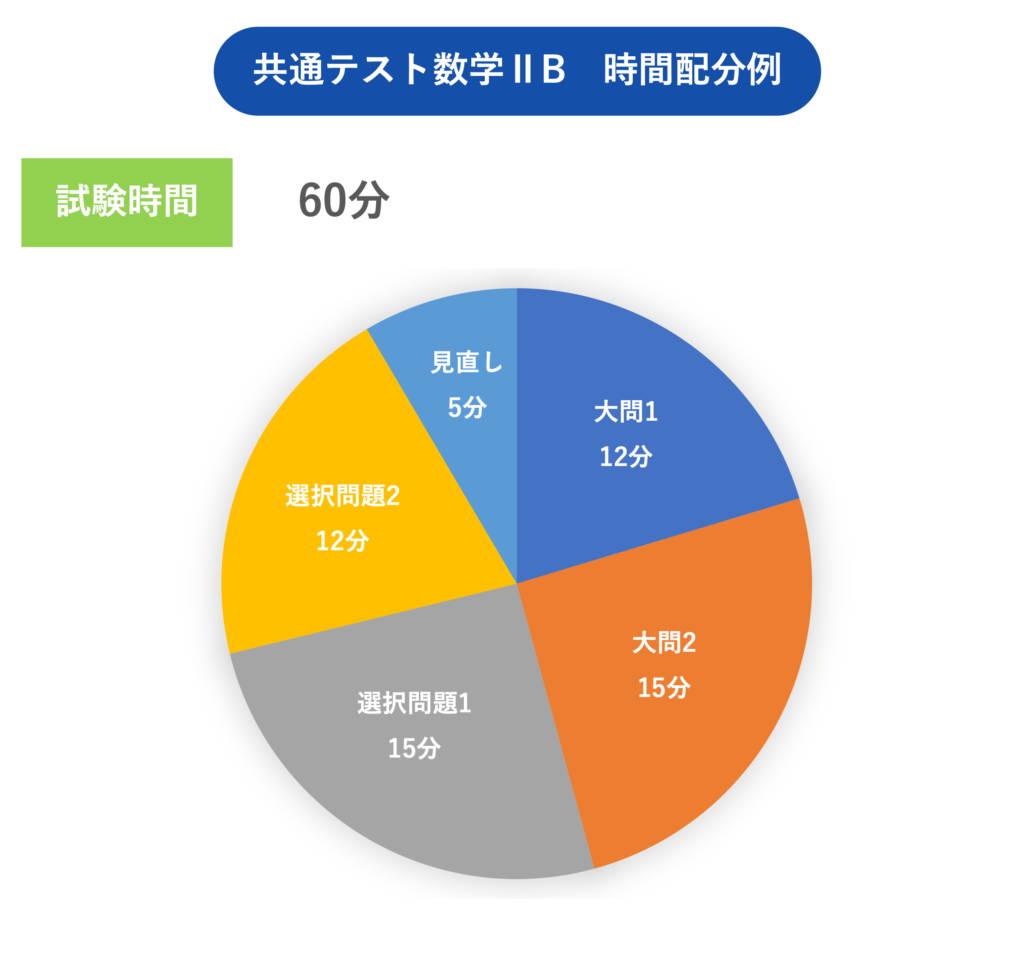
共通テスト数学ⅡB 時間配分例
数学IIBの時間配分例は下記のとおり。
試験時間は60分。
ⅠAとは試験時間が異なります。
見直し・チェックは余裕を持って行いたいところなので、時間を短縮できるよう工夫が必要です。
数学ⅡB 時間配分例
|
大問1 |
12分 |
|---|---|
|
大問2 |
15分 |
|
選択問題1 |
15分前後 |
|
選択問題2 |
12分前後 |
|
見直し |
5分前後 |
|
計 |
60分 |
ⅠA・ⅡBともに、設問別の時間配分の目安を記載しますが、あくまで目安の為、得意な問題傾向の設問は時間を短縮して、苦手問題傾向の設問には時間を余分にとるなどの調整は必要になります。あと、見直しの時間も最初から考慮した時間配分で取り組めるとミスもなくなり高得点に繋がります。
読解が必要な応用問題に十分時間をかけられるようにするためにも、典型問題を素早く正確に解く練習が必要といえます。
過去問や予想問題などで解き方のコツをつかもう
時間内に解ききるためのコツをいくつかご紹介します。
設問・選択肢を先に読む
まず設問・選択肢を先に読んで、「何が問われているか」を把握したうえで問題文を読みましょう。
わからない問題はとばす
わからない問題にこだわって時間がなくなってしまうとあとの大問をまるまる解けないということもありえます。
わからない問題は潔く飛ばして、解ける問題や時間をかけたら解ける可能性のある問題から解いていきましょう。
2025年度共通テスト数学の試験で満点を目指すには?独学勉強法
共通テスト数学で9割以上を目指す・満点を目指すのであれば、まずは基本的な解法はすべておさえる・覚えることが大前提です。そのうえでその解法を使いこなせるようにしましょう。どの問題が出てきたらどの公式・解法を使うのかを掴むことが大切です。問題集や参考書を使って問題をたくさん解き、着眼点とそれに対応する公式・解法を整理しましょう。また、ふだんの学習時に問題と答えだけでなく、関連事項やコラムも含めて数学の文章を読み慣れていると有利です。
そこまでできれば、あとは素早く解くトレーニングに移ります。過去問や模試などを活用し、本番に焦ってしまわないように、余裕を持って解ききれるくらいまで演習を繰り返しましょう。
数学以外の他教科の大学入学共通テスト対策
基礎的な知識が身についていることを前提に、思考力や応用力を問われるというのが全教科・科目を通じての共通テストの傾向となっています。
他教科の共通テストの科目別問題傾向と対策も詳しく説明していますので、是非参考にして共通テスト対策の勉強を進めていきましょう。
共通テストを完全攻略できる学習に取り組んでみませんか?